Lisa’s Method: A New Arrangement For Finding Slope
The National Council of Teachers of Mathematics continues to advocate for more student-centered mathematics teaching (NCTM, 2000). One of my dreams as a mathematics teacher and tutor is to have a student come up with an innovative approach to doing or thinking about some mathematics. And one of my nightmares is hearing of or seeing a student do something creative and be ignored or slapped down by an insensitive or ignorant instructor who fails or fears to consider that a student’s ideas about something might be of value. One of the worst aspects of “sage on the stage” mathematics teaching is its propensity for minimizing opportunities for students to do any thinking in class that strays from the teacher’s directed and generally very beaten path.
Recently, I had one of those much-desired opportunities to see a student spontaneously come up with what was, to me at least, an original approach to something that is easy for and familiar to many, but distressingly hard for a significant number of students: calculating the slope of a straight line given two points. My student, Lisa, had been working her way through a computer-based first semester geometry course and came to me unsure about how to find slope. As I anticipated, her problem centered the question of where to put the x- and y-coordinates in the slope equation. She was given the points (3, 2) and (-2, -4) with a picture of the graph, so I began by asking if she could tell from the graph whether the slope would be positive or negative. Once she was clear that the slope of a line that went up from left to right had to be positive, which was indeed the case with the line in question, I modeled for her how to draw a right triangle by extending a vertical segment down from (3,2) and a horizontal one to meet it from (-2, -4). I then asked her to find the lengths of the two legs of this triangle (5, and 6, respectively): an advantage for many students of this graphical approach is that lengths are positive regardless of the presence of negative numbers amongst the coordinates, and it is relatively easy for them to see or be convinced that adding the distances left and right or above and below the axes, respectively, as all positive numbers will get the correct lengths.
We then turned to the question of which of these numbers was the numerator of the slope. I offered the idea that slope represents a ratio of change between the vertical change of the line, positive, negative or zero, to its horizontal change from left to right, using the notation Dy/Dx, which Lisa responded to as something she knew from her physical science courses, stating, “Yes, that was how Ms. Acree [her science instructor] showed me.” I wasn’t sure, however, if Lisa saw that this was just a compact way of showing what we had looked at graphically, as well as indicating what calculations had to be done. When I asked if she knew what to do next, she said, “I’m not really certain.” I wrote Dy/Dx = (y2 - y1)/(x2 - x1) and asked her if that made sense. At that point, she said, “Oh, now I see why I keep getting the problems wrong: I’m putting the x’s on the top.”
Of course, this error is one all-too-familiar to mathematics instructors around the world. Countless students have lost untold numbers of points on exams due to this simple and understandable error. After all, x comes before y in the alphabet. And the x-coordinate precedes its partner y-coordinate in every ordered pair. Why wouldn’t it “come first” when writing the ratio for slope?
While we can all sagely agree that students “shouldn’t” make this error based on the underlying meaning of slope, as I pointed out to Lisa before going to notation, it is useless to speak about what is supposed to happen given what so often does. Much as it is important to try to get students to think clearly about the meaning of the mathematics they write and calculate with, it is difficult to ensure that this particular error, one I sometimes start to make myself if I’m not careful, does not occur.
To check her understanding, I posed a second problem to Lisa, giving her the points (3, 9) and (1, 1). She solved the problem graphically first, but was still a little unsure about doing it algebraically, so I did the usual set-up, writing m = (9 - 1)/(3 - 1) = 8/2 = 4.
Lisa looked at what I’d written down and suddenly took the paper and wrote something down, saying, “Couldn’t you do it like this?” (See Fig. 1)

Fig 1: Lisa’s Method
After looking at this for a few seconds, I thought that I understood what Lisa’s intentions were. However, I could see problems with her notation. To check, I asked what the symbols between the numbers in parentheses meant and she made clear to me that they were dashes, not subtraction signs. I asked about the slash and she said, “Oh, that means that you divide the two into the eight to get four, which would be the slope.”This was what I thought she meant, but I asked her if it seemed possible that most people would be confused by what seemed like indicated subtractions, and if she felt that math teachers would be very distressed by the idea that what she’d written at the bottom should be read the way she intended. She said, “Oh, I see what you mean about the dashes. But I don’t see what’s wrong with the bottom part.”
I said that in fact she appeared to be claiming that two divided by eight equaled four rather than one-fourth. But I believed that I saw an easy fix to what she had done. I then wrote below her figure (see Fig. 2)
This seemed more consistent with what was intended and didn’t use any non-standard or misleading notation. I asked Lisa if what I had done made clear what she wanted; she agreed that it did. The logical continuation would then be to perform the indicated division to get the slope (See Fig. 3)

Fig. 3 Teacher’s Version Completed
This correctly completed the solution for finding the slope of the line that contained the two given points.Lisa said she agreed with the changes I’d made. At this point, I said: “I have never seen anyone find slope like this. Did another teacher show you this?” She answered, “No, but when I saw how you did it, it just seemed to me that this would work. It seemed natural to me.”
I asked her explain why this seemed like a good way to her. She said, “Well, we always did subtraction problems like that: it seems easier to me when the numbers are lined up this way.”
I told her that I thought she might have invented an original approach that made sense, and that I was going to write up what she’d done for publication so that other teachers would have a chance to share it with their students. I think she believed I was pulling her leg, and though I tried to make clear that I was serious, even when I told her again at the end of class that I was definitely impressed by her approach and was going to write it up, she appeared skeptical.
What seems useful about Lisa’s method is that it solves the typical problem of forcing students to put the y-coordinates “first,” out of alphabetical order, when they may still be struggling to simply get a handle on what slope is and how to interpret it. So many students learn (and are often taught) mathematics in a mechanical, procedural way, and in the case of calculating slope, there is something counterintuitive about how we set up the ratio, even though we would like it to make sense. Clearly, solving the problem using her approach avoids putting students in a position where many will lose points on exams and become frustrated with this vital part of dealing with linear equations and their graphs. In the long run, I would expect that when they have a firmer understanding of slopes as ratios of change and of what it is that is changing relative to what (dependent variable relative to unit change in independent variable), they will become more comfortable and effective with the traditional approach. And of course, some students will be perfectly fine with the usual way of finding slope and will likely eschew Lisa’s alternative. However, as another possible way to set up this important calculation, it seems to have promise for struggling students.
Of course, I don’t mean to suggest that her method (or any approach) is a panacea for all possible student difficulties. Naturally, students still need to know how correctly subtract signed numbers. While my work with Lisa suggested that she was comparatively clear on integer arithmetic (based on work we did previously), most of my students are typical in struggling greatly with both the procedures and concepts in this regard. That is one reason I would strongly suggest that teachers have students find slopes of lines with points in the first quadrant and/or on the axes defining that part of the Cartesian plane. Further, it seems an aid to reviewing the requisite arithmetic to then have students solve problems graphically (using right triangles as I demonstrated to Lisa) before doing the symbolic arithmetic when including points in the other three quadrants.
For Lisa, the question of finishing the problem with dividing a smaller positive integer into a larger one was unproblematic. Further experimentation with numbers of opposite signs or with two negative numbers caused her no difficulty either, and she successfully concluded in cases that resulted in both proper and improper fractions that as long as she reduced to lowest terms, no further adjustment was needed to the results she calculated with her method. However, it is not at all obvious that this would be the case for all students, so further investigation along these lines will be important.
If nothing else, what Lisa has done can be shown to students as an example of creative solutions to simple but annoying sticking places for many teachers and students. I’ve personally never been happy with the “rise over run” idea, though I offer it to students as a mnemonic, because the word “run” doesn’t communicate horizontal motion to me clearly, even though it does to some students. I also worry sometimes that it locks students into thinking of slope too literally as restricted to a graphical interpretation, rather than keeping open the idea of slope as a ratio of change between dependent and independent variables.
Lisa seems to have spontaneously created something that for me might solve a nagging pedagogical problem: how to teach students to calculate the slope of a line from two given points without having to do something that for many does not come naturally. The key here for me (and I hope for teachers reading this article) is that I was open to seeing Lisa’s ideas and that we had established the kind of relationship where she felt comfortable sharing what seemed like a spontaneous burst of creativity with me. While it is far easier to be receptive to student thinking in the one-on-one teaching I often do as a consultant, coach, guest teacher, or in full-time work as a Title I mathematics teacher, I believe it is vital that teachers in more typical group and whole-class teaching situations remain open to opportunities to explore student ideas. As the work of teachers like Ball (1993) and Lampert (1985) shows, teachers must make dozens of decisions about such moments, and it is easy to lose them under the pressure to “cover the curriculum.” But if we are serious about teaching mathematics in ways that value and promote independent student thinking and active participation in a mathematical learning community, we cannot afford to miss the unexpected. At worst, we need to note when students have provocative, promising mathematical ideas so that we can revisit them later with their authors and other students. It’s not always possible in the heat of a lesson to see whether an idea warrants taking a detour from the official planned route. Even if something needs to be put on the back burner, it is important that students know that their ideas are valued, and vital that the teacher get back to the student to discuss and explore such insights and speculations further. And of course, it is necessary that teachers have adequate mathematical knowledge to recognize the potential significance of their students’ ideas (Ball, et al, 2005). But the more teachers take their students seriously as sources of rich mathematical ideas, the more likely it is that students will engage more fully in mathematics and indeed produce surprising and fruitful ideas.
References
Ball, D. L., Hill, H.C, & Bass, H. (2005). Knowing mathematics for teaching: Who knows mathematics well enough to teach third grade, and how can we decide? American Educator.Ball, D. L. (1993). With an eye on the mathematical horizon: Dilemmas of teaching elementary school mathematics. Elementary School Journal, 93 (4), 373-397.
Lampert, M. (1985). How do teachers manage to teach?: Perspectives on problems in practice. Harvard Educational Review , 55 (2), 178-194.
National Council of Teachers of Mathematics (NCTM). Principles and Standards for School Mathematics. Reston, VA: NCTM, 2000.
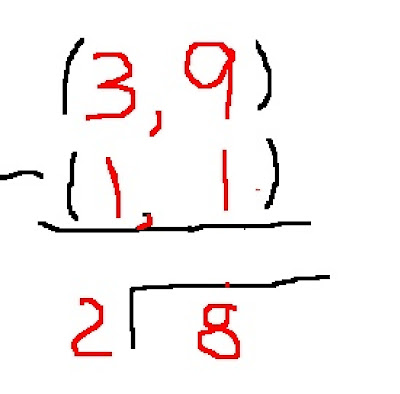
No comments:
Post a Comment